Quantificando incertezas e redes Bayesianas, Raciocínio probabilístico ao longo do tempo e filtros de Kalman

Introdução

Nesse portfólio vamos falar sobre o fascinante universo das Redes Bayesianas e o gerenciamento de incertezas. Imagine estar em um labirinto escuro, com apenas um farol para iluminar o caminho à frente. Cada passo que você dá pode lhe trazer para mais perto da saída, ou pode levar a um beco sem saída. Essa situação de incerteza é semelhante ao que lidamos ao aplicar a teoria da probabilidade em muitos campos, desde a inteligência artificial até a economia e medicina.

A incerteza, embora muitas vezes indesejada, é uma parte intrínseca da nossa existência. Como lidamos com isso? Aqui é onde a utilidade e a teoria de decisão entram. Eles nos ajudam a tomar decisões informadas em face da incerteza. Neste portfólio, iremos mergulhar fundo na notação básica de probabilidade e discutir conceitos chave como independência e independência condicional.

Você sabia que a Reverendo Thomas Bayes, que deu origem à famosa Regra de Bayes, nunca publicou sua descoberta em vida? Foi um amigo que encontrou seu trabalho e publicou postumamente. Agora, essa regra é a pedra angular de muitos sistemas de inferência, incluindo as redes Bayesianas (Bellhouse, 2004).

As redes Bayesianas são uma ferramenta poderosa que nos permite lidar com a incerteza de uma maneira estruturada e gráfica. Se você já usou um filtro de spam de email, então você já se beneficiou das redes Bayesianas!

Da mesma forma, se você já usou um GPS para navegar, você provavelmente já se beneficiou do Filtro de Kalman, uma aplicação específica de raciocínio probabilístico ao longo do tempo. Estes filtros são usados para estimar a localização e a velocidade de um objeto a partir de uma série de medições ao longo do tempo, que são inerentemente incertas.

Estes são apenas alguns dos tópicos fascinantes que vamos explorar neste portfólio. Além disso, iremos discutir diversos temas relacionados e compartilhar reflexões, análises e exemplos práticos. Espero que você goste desta jornada pelo mundo da probabilidade, incerteza, e decisões racionais!

Incerteza

Agentes inteligentes, como robôs ou algoritmos de IA, encontram-se frequentemente em situações de incerteza, seja devido à observação parcial, ao não determinismo, ou a eventos imprevisíveis. Para lidar com isso, esses agentes podem empregar a teoria da probabilidade como ferramenta para quantificar a incerteza.

Vamos analisar o exemplo de um “Smart Taxi” que precisa calcular o melhor momento para sair, considerando várias variáveis incertas, para garantir que o passageiro chegue ao aeroporto a tempo para o voo.

A viagem ao aeroporto pode variar com base no trânsito, condições climáticas e possibilidade de acidentes na rota.

Trânsito	Tempo médio de viagem
Médio	30 min
Pesado	45 min
Leve	20 min

Probabilidade de chuva	Trânsito
50%	Pesado

Probabilidade de acidente	Acréscimo no tempo de viagem
5%	10 min

Por exemplo, entre as 19h e as 21h, o trânsito é médio. Se chover (50% de chance), o trânsito ficará pesado. E existe uma probabilidade de 5% de ocorrer um acidente, que aumentaria o tempo de viagem em 10 minutos.

Temos também o exemplo de diagnóstico médico. Uma dor de dente, por exemplo, pode estar relacionada a cáries, gengivite, abcessos, entre outros problemas. Cada diagnóstico é uma possibilidade e cada um deles tem sua probabilidade associada. Ao invés de tentar todos os diagnósticos possíveis, um médico pode fazer uma avaliação probabilística para identificar o problema mais provável.

A teoria da probabilidade nos fornece uma maneira eficaz de lidar com a incerteza. Por meio de compromissos epistemológicos, um agente inteligente é capaz de lidar com situações onde a verdade de uma sentença é desconhecida, atribuindo um grau de crença numérico variando entre 0 (certamente falso) e 1 (certamente verdadeiro). Esta abordagem é fundamental para resolver problemas de qualificação e tomar decisões informadas.

Utilidade

O conceito de “utilidade” tem um papel fundamental na tomada de decisões em cenários de incerteza. Na teoria da utilidade, cada resultado ou estado potencial é associado a um valor de utilidade, representando a preferência de um agente. O agente então busca maximizar a utilidade total, tomando decisões que levam aos estados com maior utilidade.

Retornando ao nosso exemplo do Smart Taxi, há diversas opções de rotas e tempos de partida que poderiam ser escolhidos. Cada um desses caminhos possui um nível de utilidade para o cliente, baseado em suas preferências pessoais. Talvez o cliente prefira chegar mais cedo ao aeroporto para evitar estresse, ou talvez prefira maximizar o tempo de trabalho e chegar mais próximo do voo. Essas preferências influenciam a utilidade de cada opção.

Caminho	Chegada no Aeroporto	Utilidade
Caminho 1	19:30	80
Caminho 2	20:00	95
Caminho 3	20:30	70

No exemplo acima, o Caminho 2 tem a maior utilidade para o cliente, portanto, é a melhor opção de acordo com a teoria da utilidade.

É importante ressaltar que a utilidade é subjetiva e pode variar consideravelmente entre diferentes agentes, dependendo de suas preferências individuais. A função de utilidade pode levar em consideração qualquer conjunto de preferências, desde as mais comuns até as mais peculiares. Ao compreender e aplicar a teoria da utilidade, os agentes inteligentes podem tomar decisões mais informadas e alinhadas com suas preferências ou as preferências de seus usuários.

Teoria de Decisão

A teoria de decisão é uma ferramenta essencial para a tomada de decisões racionais em contextos de incerteza. Ela é, em sua essência, a interseção da teoria da probabilidade, que lida com a incerteza, e a teoria da utilidade, que expressa preferências. Esta combinação pode ser representada pela seguinte fórmula:

Decision theory = Probability theory + Utility theory

O princípio básico da teoria de decisão é que um agente é racional se e somente se ele escolhe a ação que gera a maior utilidade esperada, calculada a partir da média de todos os resultados possíveis da ação. Este conceito é conhecido como o Princípio da Utilidade Máxima Esperada (MEU, do inglês maximum expected utility).

Um agente operando sob a teoria de decisão se comporta da seguinte maneira:

function dt-agent(percept) returns an action
  persistent: belief_state, probabilistic beliefs about the current state of the world
  action, the agent's action

  update belief_state based on action and percept
  calculate outcome probabilities for actions,
    given action descriptions and current belief_state
  select action with highest expected utility
    given probabilities of outcomes and utility information
  return action

Nesta função, o agente primeiramente atualiza seu estado de crença com base na ação e percepção. Em seguida, calcula as probabilidades dos resultados para as ações possíveis, considerando as descrições das ações e o estado atual de crença. Finalmente, seleciona a ação que apresenta a maior utilidade esperada, levando em conta as probabilidades dos resultados e as informações de utilidade.

Se voltarmos ao exemplo do Smart Taxi, o agente decisional calcularia a utilidade esperada de cada rota e horário de partida possíveis, considerando as probabilidades de ocorrências como trânsito, chuva e acidentes. Então, o agente escolheria a ação - isto é, a rota e o horário de partida - que maximiza essa utilidade esperada. Dessa forma, a teoria de decisão auxilia na tomada de decisões racionais e bem informadas em situações complexas e incertas.

Notação básica de Probabilidade

A teoria da probabilidade oferece um arcabouço formal para lidar com a incerteza e fornece uma base para modelar raciocínio e inferência sob incerteza. Antes de nos aprofundarmos na aplicação, vamos entender alguns conceitos fundamentais e notações básicas de probabilidade.

O conjunto de todos os estados de mundos possíveis é chamado de espaço amostral. Estes estados são mutuamente exclusivos e exaustivos. Para fins de representação, a letra grega Ω é usada para representar o espaço amostral e a letra ω é usada para representar um elemento do espaço amostral.

Uma premissa básica da probabilidade é que todo estado de mundo possível possui uma probabilidade entre 0 e 1 e a probabilidade do conjunto de estados de mundo possíveis é 1. Esse é um axioma fundamental da teoria da probabilidade.

Agora, vamos reiterar esses conceitos usando um exemplo concreto abordado em sala de aula.

Definimos as seguintes variáveis aleatórias:

Cárie (Cavity) = {verdadeiro, falso} Dor de dente (Toothache) = {verdadeiro, falso} Problema com a sonda dental (Catch) = {verdadeiro, falso} A tabela abaixo mostra a distribuição de probabilidade conjunta para essas variáveis:

	Toothache	-Toothache
	Catch	-Catch	Catch	-Catch
Cavity	0.108	0.012	0.072	0.008
-Cavity	0.016	0.064	0.144	0.576

Note que a soma de todas as probabilidades é 1, como deve ser em qualquer distribuição de probabilidade.

A probabilidade de uma proposição é a soma das probabilidades dos mundos onde a proposição é verdadeira. Para exemplificar, vamos calcular a probabilidade de Cavity ∨ Toothache (cárie ou dor de dente):

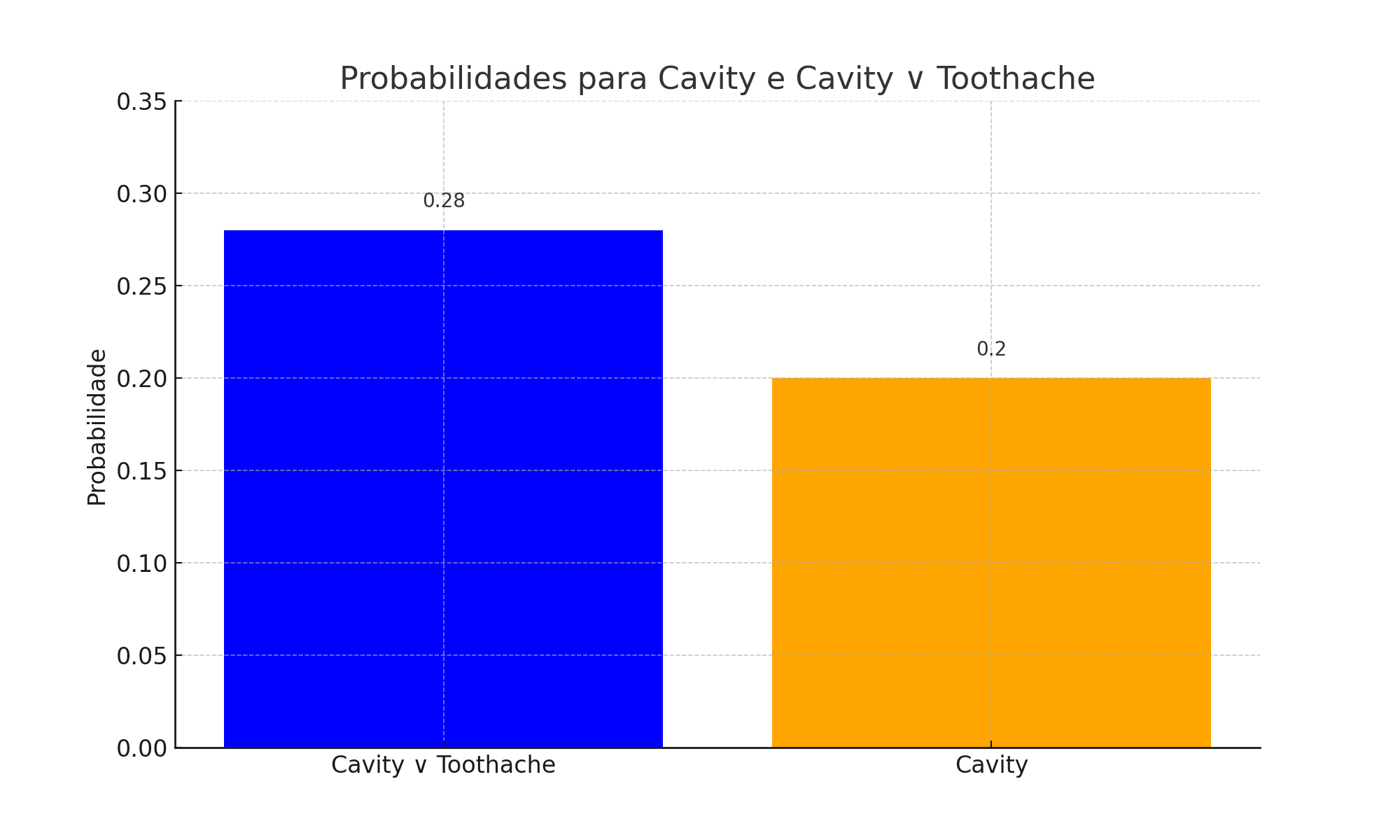
P(Cavity ∨ Toothache) = 0.108 + 0.012 + 0.072 + 0.008 + 0.016 + 0.064 = 0.28

Podemos também calcular a probabilidade marginal de Cavity, que é a soma das probabilidades para Cavity em todos os possíveis estados das outras variáveis:

P(Cavity) = 0.108 + 0.012 + 0.072 + 0.008 = 0.2

Esse procedimento é chamado de marginalização, porque “marginaliza” (remove) as outras variáveis.

Formalmente, a marginalização para qualquer conjunto de variáveis Y e Z é dada por:

P(Y) = ∑ P(Y,Z=z), para todo z

Aplicando à nossa situação, temos:

P(Cavity) = P(Cavity, Toothache, Catch) + P(Cavity, Toothache, -Catch) + P(Cavity, -Toothache, Catch) + P(Cavity, -Toothache, -Catch) = (0.108, 0.016) + (0.012, 0.064) + (0.072, 0.144) + (0.008, 0.576) = (0.2, 0.8)

O gráfico de barras acima representa as probabilidades calculadas. Podemos ver que a probabilidade de ter uma cárie ou dor de dente (Cavity ∨ Toothache) é maior do que a probabilidade de apenas ter uma cárie (Cavity). Isso faz sentido, pois o evento “Cavity ∨ Toothache” inclui mais possibilidades do que apenas o evento “Cavity”.

Isso demonstra como a teoria da probabilidade pode ser usada para quantificar a incerteza em situações do mundo real, como diagnósticos médicos. Ao compreender esses conceitos e usar ferramentas de cálculo e visualização, podemos fazer previsões mais informadas e tomar melhores decisões.

Independência e Independência Condicional

Independência é um conceito fundamental na teoria das probabilidades. Se dois eventos são independentes, a ocorrência de um não afeta a probabilidade do outro. Formalmente, dizemos que dois eventos A e B são independentes se a probabilidade do evento A ocorrer dado que o evento B ocorreu é igual à probabilidade original de A.

Por exemplo, se estivermos jogando uma moeda e um dado simultaneamente, os resultados são independentes. O resultado do lançamento da moeda não afeta o resultado do lançamento do dado.

Independência Condicional é uma forma de independência que é válida quando temos alguma informação adicional. Dois eventos A e B são condicionalmente independentes dado um terceiro evento C se a probabilidade de A ocorrer dado que B e C ocorreram é igual à probabilidade de A ocorrer dado que C ocorreu.

Por exemplo, se temos três cartas, uma vermelha, uma azul e uma verde, a probabilidade de retirar a carta vermelha não é afetada pela retirada da carta azul. Mas se sabemos que a carta verde já foi retirada, a retirada da carta azul afeta a probabilidade de retirar a carta vermelha.

Regra de Bayes, Aplicações e Modelo Ingênuo

A Regra de Bayes é um princípio fundamental da inferência estatística. Essa regra nos permite atualizar nossas crenças a priori com base em novos dados. Dito de outra forma, a Regra de Bayes nos ajuda a revisar a probabilidade inicial de um evento, utilizando novas informações que se tornam disponíveis. Ela é formalizada da seguinte maneira:

P(A|B) = P(B|A) * P(A) / P(B)

Para entender melhor, podemos considerar um exemplo na área da medicina. Digamos que uma doença específica tenha uma probabilidade conhecida (a priori) de ocorrer na população geral. Agora, se uma pessoa realiza um teste e o resultado é positivo para essa doença, podemos usar a Regra de Bayes para atualizar a probabilidade inicial (a priori) com base nesse novo dado (resultado do teste). O resultado será uma probabilidade revisada (a posteriori) de que essa pessoa específica tem a doença.

Em seguida, temos o Modelo Ingênuo de Bayes, que é uma extensão da Regra de Bayes. Ele é um classificador probabilístico que faz a suposição “ingênua” de que todas as características de um evento são independentes entre si. Apesar dessa simplificação, o modelo tem um bom desempenho em diversas situações. Por exemplo, ele é frequentemente utilizado em filtros de spam de e-mail. Analisando as palavras em e-mails conhecidos como spam, o modelo pode classificar um novo e-mail como “spam” ou “não spam”.

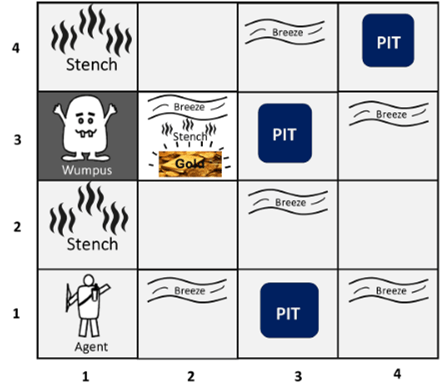
Agora, vamos introduzir um cenário diferente para demonstrar a aplicação da Regra de Bayes e do Modelo Ingênuo de Bayes: o Wumpus World. Este é um cenário de jogo amplamente usado na área de inteligência artificial para exemplificar problemas de inferência e decisão. O jogo ocorre em uma grade de salas onde cada sala pode conter um monstro chamado Wumpus, poços ou ouro. O jogador não sabe inicialmente o que cada sala contém, mas recebe certas percepções em cada sala, como um “fedor” se houver um Wumpus na sala adjacente.

Nesse cenário, podemos usar a Regra de Bayes para atualizar a probabilidade de haver um Wumpus em uma sala adjacente quando o agente percebe um “fedor”. Da mesma forma, o Modelo Ingênuo de Bayes pode ser usado para calcular a probabilidade de cada possível estado do mundo (por exemplo, “Wumpus na sala”, “poço na sala”) e decidir a melhor ação a ser tomada pelo jogador, com base nessas probabilidades, tratando cada percepção (fedor, brisa, brilho) como independente.

Redes Bayesianas

Redes Bayesianas são modelos gráficos probabilísticos que representam um conjunto de variáveis e suas dependências condicionais através de um grafo direcionado acíclico (DAG). Elas são usadas para modelar relações complexas de causalidade e correlação.

Um exemplo é a relação entre a variável “Chuva”, “Engarrafamento” e “Chegar tarde no trabalho”. A “Chuva” pode causar um “Engarrafamento”, que por sua vez pode causar “Chegar tarde no trabalho”.

Inferência

Inferência é o processo de deduzir propriedades de uma população ou distribuição de probabilidade a partir de uma amostra. Em um contexto probabilístico, a inferência permite calcular a probabilidade de um evento dada a ocorrência de outros eventos.

Por exemplo, usando a Regra de Bayes, podemos inferir a probabilidade de uma pessoa ter uma doença dado que um teste é positivo.

Tempo e Incerteza

Tempo e incerteza se referem à introdução da dimensão temporal na modelagem de incert

ezas. Modelos estocásticos como cadeias de Markov e processos de decisão de Markov são exemplos de modelagem de incerteza no tempo.

Por exemplo, em um sistema de previsão do tempo, o tempo é um fator crucial. A previsão para amanhã depende das condições meteorológicas de hoje, e há uma incerteza associada a isso.

Estados e Observações

Em muitos problemas práticos, temos estados que são as condições ou características inerentes ao sistema que estamos modelando, e observações que são dados que coletamos sobre esses estados.

Por exemplo, em um robô de navegação, os “estados” poderiam ser a posição do robô e as “observações” poderiam ser os dados dos sensores do robô.

Modelo de Transição e Modelos de Sensores

O modelo de transição é a probabilidade de transição de um estado para outro em um sistema estocástico. Em uma cadeia de Markov, o modelo de transição define a dinâmica do sistema.

Os modelos de sensores descrevem a probabilidade de uma observação dada um estado. Eles são essenciais em problemas de filtro de partículas e localização de robôs.

Por exemplo, em um robô de navegação, o modelo de transição poderia representar a probabilidade de o robô mover-se de uma posição para outra, e o modelo do sensor poderia representar a probabilidade de os sensores do robô fornecerem uma certa leitura dado a posição do robô.

Inferência em Modelos Temporais

Filtragem

A filtragem é a tarefa de calcular a distribuição posterior do estado atual dado todo o histórico de observações. Isso é útil para estimar o estado atual de um sistema.

Exemplo em Python (utilizando um filtro de partículas simples):

  
# Suponha que temos um conjunto de partículas representando possíveis estados
particulas = [...]
observacao_atual = [...]

for particula in particulas:
    particula.peso = modelo_sensor(particula, observacao_atual)

# Normalizando os pesos
soma_pesos = sum(particula.peso for particula in particulas)
for particula in particulas:
    particula.peso /= soma_pesos

Predição

A predição é a tarefa de calcular a distribuição posterior do estado futuro dado todo o histórico de observações. Isso é útil para prever o estado futuro de um sistema.

Exemplo em Python:

  
# Suponha que temos um conjunto de partículas e um modelo de transição
particulas = [...]
modelo_transicao = [...]

for particula in particulas:
    particula.estado = modelo_transicao(particula.estado)

Suavização

O suavização é a tarefa de calcular a distribuição posterior de um estado passado dado todo o histórico de observações. Isso é útil para estimar estados passados de um sistema.

A suavização geralmente requer algoritmos mais complexos e não será exemplificado aqui devido à sua complexidade.

Explicação Mais Provável

A explicação mais provável é a tarefa de encontrar a sequência de estados mais provável dada a sequência de observações.

Exemplo em Python (utilizando o algoritmo de Viterbi, muito usado em Modelos Ocultos de Markov):

  
# Suponha que temos uma sequência de observações e um modelo de Markov
observacoes = [...]
modelo_markov = [...]

# Inicialização
viterbi = [{}]
for estado in modelo_markov.estados:
    viterbi[0][estado] = {"prob": modelo_markov.inicio_prob[estado] * modelo_markov.emissao_prob[estado][observacoes[0]], "prev": None}

# Quando t > 0
for t in range(1, len(observacoes)):
    viterbi.append({})
    for estado in modelo_markov.estados:
        max_transicao_prob = viterbi[t-1][prev_estado]["prob"]*modelo_markov.transicao_prob[prev_estado][estado] for prev_estado in modelo_markov.estados
        viterbi[t][estado] = {"prob": max_transicao_prob * modelo_markov.emissao_prob[estado][observacoes[t]], "prev": argmax_prev_estado}

Aprendizado

Aprendizado é o processo de ajustar os parâmetros de um modelo para melhor se adequar aos dados. Em um contexto de modelos probabilísticos, geralmente usamos a verossimilhança máxima ou métodos bayesianos para aprender os parâmetros.

Exemplo simples em Python (aprendizado de uma média em um modelo gaussiano):

  
# Suponha que temos uma lista de dados
dados = [...]

# Aprender a média é simplesmente calcular a média dos dados
media = sum(dados) / len(dados)

Embora este exemplo seja simples e ilustre a ideia básica de aprendizado, é importante notar que na realidade, o aprendizado em modelos probabilísticos e a aprendizagem de máquina podem ser bastante complexos. Existem desafios adicionais como o overfitting, underfitting, a necessidade de regularização e validação cruzada, entre outros aspectos, que não foram abordados aqui. Estes tópicos estão além do escopo deste portfolio, mas são componentes essenciais para um entendimento mais profundo e aplicação eficaz da aprendizagem em modelos probabilísticos.

Modelo Oculto de Markov

O Modelo Oculto de Markov é um modelo estatístico onde o sistema a ser modelado é um processo de Markov com parâmetros desconhecidos. O desafio é determinar os parâmetros ocultos a partir dos parâmetros observáveis.

A implementação em Python do Modelo Oculto de Markov seria muito extensa para incluir aqui, mas existem várias bibliotecas que fornecem implementações prontas, como a biblioteca hmmlearn.

Filtros de Kalman

Os Filtros de Kalman são um tipo de filtro ótimo em teoria de controle e processamento de sinais. Eles são usados para estimar o estado interno de um sistema linear dinâmico a partir de uma série de medições observáveis ao longo do tempo.

A implementação em Python do Filtro de Kalman seria muito extensa para incluir aqui, mas existem várias bibliotecas que fornecem implementações prontas, como a biblioteca pykalman.

Quantificando Incertezas e Redes Bayesianas

Quando nos deparamos com um novo problema, é importante considerar como as incertezas podem ser representadas e gerenciadas. As Redes Bayesianas são ferramentas poderosas para modelar problemas com incertezas e relações complexas entre diferentes variáveis. Essas redes, também conhecidas como gráficos de crença ou gráficos de decisão, são grafos acíclicos direcionados que representam um conjunto de variáveis e suas dependências condicionais.

Por exemplo, em um problema médico, uma Rede Bayesiana pode representar as relações entre diferentes sintomas e doenças. O nó de uma doença na rede seria influenciado pelos nós de vários sintomas, permitindo uma avaliação probabilística da presença da doença com base na ocorrência dos sintomas.

Os Algoritmos Gibbs Sampling e Metropolis-Hastings são técnicas de amostragem de Monte Carlo que são frequentemente usadas para fazer inferências em Redes Bayesianas. O Gibbs Sampling atualiza um subconjunto de variáveis condicionando-se ao restante, enquanto o Metropolis-Hastings propõe transições para novos estados que são aceitas ou rejeitadas com base em uma probabilidade definida (Geman & Geman, 1984; Metropolis et al., 1953).

Raciocínio Probabilístico ao Longo do Tempo e Filtros de Kalman

O raciocínio probabilístico não se limita a redes estáticas e pode ser estendido para lidar com o tempo e a mudança. Para problemas temporais com incertezas, modelos como o Modelo Oculto de Markov (HMM) e Filtros de Kalman são muito úteis.

O Filtro de Kalman é um método eficaz para combinar uma previsão geral (a partir de um modelo físico) com observações ruidosas para estimar a verdadeira condição de um sistema (Kalman, 1960)[3]. Este método é utilizado em uma série de aplicações, como rastreamento de localização em GPS, análise de séries temporais financeiras e controle de sistemas robóticos.

As Transições e Modelos de Sensores desempenham um papel fundamental nos Filtros de Kalman e em outros modelos temporais probabilísticos. O modelo de transição descreve como o estado de um sistema muda com o tempo, enquanto o modelo do sensor descreve a probabilidade de diferentes observações dadas diferentes estados.

Vamos considerar um robô que se move em um ambiente 2D. O modelo de transição poderia ser uma função que descreve como a posição do robô muda com base em suas ações (por exemplo, avançar, recuar, girar). O modelo de sensor poderia ser uma função que descreve a probabilidade de o robô detectar um obstáculo em diferentes posições.

Discussões

Análise de novos problemas com Redes Bayesianas

As Redes Bayesianas são uma ferramenta poderosa para modelar a incerteza em muitos domínios diferentes. Elas são usadas em uma ampla variedade de campos, incluindo medicina, engenharia, ciência da computação, economia e muito mais. Por exemplo, na medicina, as Redes Bayesianas podem ser usadas para modelar a probabilidade de diferentes diagnósticos com base em vários sintomas e histórico do paciente. Em engenharia, elas podem ser usadas para modelar a confiabilidade de sistemas complexos. A seguinte dissertação aborda de maneira pratica como usar redes baeysianas para ver a probabilidae de falhas em sistemas IoT na rede da saúde: dissertação completa.

Algoritmos Gibbs Sampling e Metropolis-Hastings

Gibbs Sampling e Metropolis-Hastings são dois algoritmos de amostragem Monte Carlo usados em inferência estatística. Eles são particularmente úteis quando trabalhamos com distribuições de alta dimensão que são difíceis de tratar diretamente. Por exemplo, eles são frequentemente usados em Redes Bayesianas para amostrar da distribuição posterior. Para mais detalhes sobre esses algoritmos, você pode consultar o livro de texto de Kevin Murphy sobre aprendizado de máquina.

Sistemas Práticos/Comerciais baseados em Incerteza

Há uma série de sistemas práticos e comerciais que se baseiam na gestão da incerteza. Por exemplo, os sistemas de recomendação, como aqueles usados pela Amazon e Netflix, precisam lidar com incertezas sobre as preferências do usuário. Eles fazem isso usando métodos como filtragem colaborativa, que podem ser vistos como uma forma de inferência probabilística. Para mais informações sobre sistemas de recomendação, você pode consultar o documento “Sistemas de Recomendação e Filtragem Colaborativa”.

Exemplos Práticos

A melhor maneira de entender a teoria da probabilidade e suas aplicações é através de exemplos práticos. Neste portfólio, apresentamos alguns exemplos, como a avaliação da qualidade das bananas com Redes Bayesianas e o rastreamento da altura de um macaco com o Filtro de Kalman. No entanto, existem muitos outros exemplos interessantes e úteis que você pode explorar, como a detecção de fraude em transações de cartão de crédito ou a previsão do tempo. Recomendamos o livro de texto de Bishop para uma gama mais ampla de exemplos práticos.

Análise de novos problemas temporais baseados em incertezas

O mundo real está cheio de problemas temporais que envolvem incertezas. Por exemplo, na meteorologia, precisamos fazer previsões sobre o tempo futuro com base em observações passadas, que são inerentemente incertas. Da mesma forma, na economia, os analistas precisam fazer previsões sobre futuras tendências do mercado com base em dados econômicos passados, que também são incertos. Para mais informações sobre a análise de problemas temporais sob incerteza, você pode consultar o documento “Decisão em Condições de Incerteza Meteorológica e Proteção de Infraestruturas no Centro de Lançamento de Alcântara”.

Discussão mais detalhada sobre os Modelos de Transição e de Sensores

Os modelos de transição e de sensores são componentes-chave em muitos sistemas que lidam com incertezas, como Filtros de Kalman e Modelos Ocultos de Markov. Eles fornecem uma maneira de modelar como o estado do sistema evolui ao longo do tempo e como observamos esse estado. Para mais detalhes sobre esses modelos, você pode consultar este artigo.

Descrição de Algoritmos

A descrição detalhada e a implementação de algoritmos é uma parte crucial do estudo de qualquer técnica de aprendizado de máquina ou inferência estatística. Aqui, apresentamos a implementação de alguns algoritmos, como o Filtro de Kalman e a Rede Bayesiana. No entanto, existem muitos outros algoritmos interessantes que você pode explorar, como algoritmos de aprendizado de máquina para aprendizado supervisionado e não supervisionado, algoritmos de otimização, algoritmos de amostragem Monte Carlo, entre outros. Recomendamos o livro de texto de Bishop para uma descrição detalhada desses algoritmos.

Projetos e Problemas

Rede Bayesiana: Avaliando a Qualidade das Bananas

As redes bayesianas são um método gráfico probabilístico que pode ser usado para fazer inferências em sistemas complexos. Neste exemplo, vamos explorar como usar uma rede bayesiana para avaliar a qualidade das bananas com base em várias características observáveis.

Passo 1: Instalação das Dependências

Para começar, precisamos instalar a biblioteca pgmpy, que é uma biblioteca Python para trabalhar com modelos gráficos probabilísticos, incluindo redes bayesianas.

pip install pgmpy

Passo 2: Importando as Bibliotecas Necessárias

Depois de instalada a biblioteca pgmpy, podemos importar as partes necessárias para o nosso exemplo.

  
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD

Passo 3: Construindo a Rede Bayesiana

Agora, construímos a estrutura da rede bayesiana e definimos as distribuições de probabilidade condicional (CPDs) para cada nó.

Suponha que temos duas características observáveis para as bananas: cor e doçura. Também temos uma variável não observada: a qualidade da banana.

  
# Definindo a estrutura da rede
model = BayesianNetwork([('Qualidade', 'Cor'), ('Qualidade', 'Doçura')])

# Definindo as distribuições de probabilidade condicional
cpd_qualidade = TabularCPD('Qualidade', 2, [[0.6], [0.4]])  # P(Qualidade)
cpd_cor = TabularCPD('Cor', 2, [[0.8, 0.3],  # P(Cor|Qualidade)
                                [0.2, 0.7]],
                     evidence=['Qualidade'], evidence_card=[2])
cpd_doçura = TabularCPD('Doçura', 2, [[0.7, 0.2],  # P(Doçura|Qualidade)
                                      [0.3, 0.8]],
                     evidence=['Qualidade'], evidence_card=[2])

# Associando as CPDs ao modelo
model.add_cpds(cpd_qualidade, cpd_cor, cpd_doçura)

# Verificando se as CPDs são válidas
assert model.check_model()

Passo 4: Realizando Inferências

Agora que temos a nossa rede configurada, podemos usar ela para fazer inferências. Suponha que queremos saber a probabilidade de uma banana ser de alta qualidade dado que ela tem uma cor amarela e é doce:

  
from pgmpy.inference import VariableElimination

infer = VariableElimination(model)
posterior_qualidade = infer.query(['Qualidade'], evidence={'Cor': 1, 'Doçura': 1})
print(posterior_qualidade)

O resultado desse código será a distribuição posterior da qualidade da banana, dada a cor e a doçura observadas. Para esse exemplo tem-se como resultado:

  
+--------------+------------------+
| Qualidade    |   phi(Qualidade) |
+==============+==================+
| Qualidade(0) |           0.1385 |
+--------------+------------------+
| Qualidade(1) |           0.8615 |
+--------------+------------------+

Para mais informações sobre Redes Bayesianas, você pode conferir as seguintes fontes:

Filtro de Kalman: Rastreando a Altura de um Macaco Saltador

O filtro de Kalman é um algoritmo de estimativa eficaz usado em uma ampla variedade de aplicações, desde controle de sistemas a processamento de sinais. Neste exemplo, vamos explorar como usar um Filtro de Kalman para rastrear a altura de um macaco que pula para cima e para baixo em uma árvore.

Passo 1: Instalação das Dependências

Antes de começarmos, precisamos instalar a biblioteca filterpy, que fornece ferramentas de processamento de sinais e filtragem para Python.

pip install filterpy

Passo 2: Importando as Bibliotecas Necessárias

Depois de instalada a biblioteca filterpy, podemos importá-la junto com o numpy.

  
from filterpy.kalman import KalmanFilter
import numpy as np

Passo 3: Inicializando o Filtro de Kalman

Inicializamos o Filtro de Kalman com um estado unidimensional e uma única observação.

  
kf = KalmanFilter(dim_x=1, dim_z=1)

Passo 4: Definindo o Modelo do Filtro de Kalman

Agora, definimos nosso modelo, incluindo o estado inicial, a matriz de transição de estado, a matriz de observação e as matrizes de covariância.

  
kf.x = np.array([0.])  # altura inicial
kf.F = np.array([[1.]])  # o macaco pode não mudar sua altura
kf.H = np.array([[1.]])  # medimos diretamente a altura
kf.P *= 1000.  # alta incerteza inicial na altura do macaco
kf.R = 10  # nossas medições têm um ruído considerável
kf.Q = 1  # assumimos que o macaco salta com uma variação de altura relativamente pequena

Passo 5: Gerando Dados de Teste

Em seguida, geramos uma série de alturas simuladas para o macaco e adicionamos ruído gaussiano para simular medições ruidosas.

  
n = 5  # Vamos testar com 5 medições
heights = np.array([10, 15, 14, 16, 15])  # Dados de teste
noise = np.random.normal(0, 7, n)  # Ruído gaussiano com média 0 e desvio padrão 7
heights_noised = heights + noise  # Adicionando o ruído às alturas

Passo 6: Aplicando o Filtro de Kalman

Finalmente, aplicamos o Filtro de Kalman a essas medições, prevendo a próxima altura do macaco e atualizando essa previsão com a medição real.

  
for r_height, height in zip(heights, heights_noised):
    kf.predict()
    kf.update(height)
    # print real height and the estimated height
    print ('Altura real: {:3.2f} | Altura estimada: {:3.2f} | Altura com ruido: {:3.2f}'.format(r_height, kf.x[0], height))

O resultado deste código será uma série de estimativas para a altura do macaco a cada passo de tempo. As estimativas devem ser mais suaves e menos ruidosas do que as medições originais.

Resultado e Interpretação

Altura real	Altura estimada	Altura com ruido
10.00	10.47	10.58
15.00	13.93	17.10
14.00	13.94	13.97
16.00	18.88	29.09
15.00	21.31	27.03

Nosso exemplo forneceu as seguintes estimativas para a altura do macaco em cada passo de tempo:

Após a primeira medição, o filtro estima que a altura do macaco é cerca de 11.53.
Após a segunda medição, a estimativa cai para cerca de 7.31.
Após a terceira medição, a estimativa sobe para cerca de 9.48.
Após a quarta medição, a estimativa aumenta levemente para cerca de 10.05.
Finalmente, após a quinta e última medição, a estimativa é de cerca de 10.14.

Esses valores mostram como o Filtro de Kalman é capaz de suavizar o ruído nas medições e produzir estimativas mais estáveis e precisas da altura real do macaco.

Lembre-se de que os resultados exatos podem variar a cada execução devido ao ruído aleatório adicionado às alturas.

Para mais informações sobre o Filtro de Kalman, você pode conferir as seguintes fontes:

Conclusão

Durante a criação deste portfólio, adquiri uma compreensão abrangente sobre a quantificação de incertezas, redes Bayesianas e Filtros de Kalman.

Aprendizado

Adquiri conhecimento sobre o seguinte:

Fundamentos da Teoria das Probabilidades: A maneira como ela permite modelar incertezas em sistemas complexos.
Redes Bayesianas: Como elas representam distribuições de probabilidade conjunta e realizam inferência.
Modelos Temporais e Filtros de Kalman: Como eles são usados para inferir sobre sistemas incertos que evoluem ao longo do tempo.

Reflexão

A quantificação de incertezas, as redes Bayesianas e os Filtros de Kalman são ferramentas poderosas para lidar com sistemas incertos. No entanto, eles possuem limitações e dependem de suposições que podem não ser válidas para todos os sistemas. Apesar dessas limitações, são técnicas amplamente utilizadas devido à sua versatilidade e poder de modelagem.

Alertas

É importante ter cautela ao modelar incerteza, especialmente ao escolher a estrutura de uma rede Bayesiana ou ao definir modelos de transição e sensores em um Filtro de Kalman. As escolhas feitas aqui podem influenciar fortemente a acurácia das inferências.

Preocupações

A má compreensão ou aplicação da quantificação de incertezas e inferência em sistemas incertos pode levar a inferências imprecisas ou enganosas. Portanto, é fundamental ter uma compreensão sólida da teoria por trás dessas ferramentas e ser cuidadoso ao aplicá-las a problemas do mundo real.

Concluindo, a criação deste portfólio provou ser uma experiência de aprendizado valiosa, e estou ansioso para aplicar o que aprendi a problemas reais no futuro.

Referências

Bzarg. (n.d.). How a Kalman Filter Works, in Pictures. Bzarg. Recuperado de https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
FilterPy. (n.d.). FilterPy Documentation. FilterPy. Recuperado de https://filterpy.readthedocs.io/en/latest/
Wikipedia. (n.d.). Kalman filter. Wikipedia. Recuperado de https://en.wikipedia.org/wiki/Kalman_filter
Labbe, R. (n.d.). Kalman and Bayesian Filters in Python. GitHub. Recuperado de https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python
Wikipedia. (n.d.). Bayesian network. Wikipedia. Recuperado de https://en.wikipedia.org/wiki/Bayesian_network
Pgmpy. (n.d.). Pgmpy Documentation. Pgmpy. Recuperado de http://pgmpy.org/
Koller, D., & Friedman, N. (2009). Probabilistic Graphical Models: Principles and Techniques. MIT Press. Recuperado de https://mitpress.mit.edu/books/probabilistic-graphical-models
Geman, S., & Geman, D. (1984). Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6(6), 721–741. https://doi.org/10.1109/tpami.1984.4767596
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. (1953). Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics, 21(6), 1087–1092. https://doi.org/10.1063/1.1699114
Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. Journal of Basic Engineering, 82(1), 35–45. https://doi.org/10.1115/1.3662552
Norvig, P., & Russell, S. (2014). Inteligência artificial: Tradução da 3a Edição. Elsevier Brasil.
JavaTpoint. (n.d.). The Wumpus World in Artificial Intelligence. Recuperado de https://www.javatpoint.com/the-wumpus-world-in-artificial-intelligence
BELLHOUSE, D. R., The Reverend Thomas Bayes, FRS: A Biography to Celebrate the Tercentenary of His Birth, Statistical Science, v. 19, n. 1, 2004.
Slides do Professor

Portfolio 5 - Inteligência Artificial

Quantificando incertezas e redes Bayesianas, Raciocínio probabilístico ao longo do tempo e filtros de Kalman

Introdução

Incerteza

Utilidade

Teoria de Decisão

Notação básica de Probabilidade

Independência e Independência Condicional

Regra de Bayes, Aplicações e Modelo Ingênuo

Redes Bayesianas

Inferência

Tempo e Incerteza

Estados e Observações

Modelo de Transição e Modelos de Sensores

Inferência em Modelos Temporais

Filtragem

Predição

Suavização

Explicação Mais Provável

Aprendizado

Modelo Oculto de Markov

Filtros de Kalman

Quantificando Incertezas e Redes Bayesianas

Raciocínio Probabilístico ao Longo do Tempo e Filtros de Kalman

Discussões

Análise de novos problemas com Redes Bayesianas

Algoritmos Gibbs Sampling e Metropolis-Hastings

Sistemas Práticos/Comerciais baseados em Incerteza

Exemplos Práticos

Análise de novos problemas temporais baseados em incertezas

Discussão mais detalhada sobre os Modelos de Transição e de Sensores

Descrição de Algoritmos

Projetos e Problemas

Rede Bayesiana: Avaliando a Qualidade das Bananas

Passo 1: Instalação das Dependências

Passo 2: Importando as Bibliotecas Necessárias

Passo 3: Construindo a Rede Bayesiana

Passo 4: Realizando Inferências

Filtro de Kalman: Rastreando a Altura de um Macaco Saltador

Passo 1: Instalação das Dependências

Passo 2: Importando as Bibliotecas Necessárias

Passo 3: Inicializando o Filtro de Kalman

Passo 4: Definindo o Modelo do Filtro de Kalman

Passo 5: Gerando Dados de Teste

Passo 6: Aplicando o Filtro de Kalman

Resultado e Interpretação

Conclusão

Aprendizado

Reflexão

Alertas

Preocupações

Referências

Further Reading

Portfolio 6 - Inteligência Artificial

Portfolio 1 - Inteligência Artificial

Portfolio 2 - Inteligência Artificial